Quantifying uncertainty
Lecture 24
Warm-up
While you wait: Participate 📱💻
Given that HW 6 will be assigned on Monday, Dec 1, what day should HW 5 be due? It will be due at 11:59 pm on the deadline we decide on.
- Sunday, Nov 30 - no change
- Monday, Dec 1 - postponed by 1 day
- Tuesday, Dec 2 - postponed by 2 days
- Wednesday, Dec 3 - postponed by 3 days
Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Announcements
- HW:
- HW 5 due [whichever date we decided on in the previous slide]
- HW 6 due at 11:59 pm on Fri, Dec 6, but will be accepted until Sun, Dec 7 at 11:59 pm without penalty
- Final exam:
- In-class only, “cheat sheet” with same specs as usual allowed
- Cumulative – will definitely have material since Exam 2, but there’s so little of it that it won’t be a huge portion of the exam
- Final exam review during reading period – date/time/location TBA
- Office hours during reading period + final exam week – schedule TBA
- Grades:
- Exam 2 in-class grades posted – can review questions in my office hours anytime before the final
- Exam 2 take-home + project grades to be posted after Thanksgiving break
Quantifying uncertainty
Goal
Find range of plausible values for the slope using bootstrap confidence intervals.
Packages
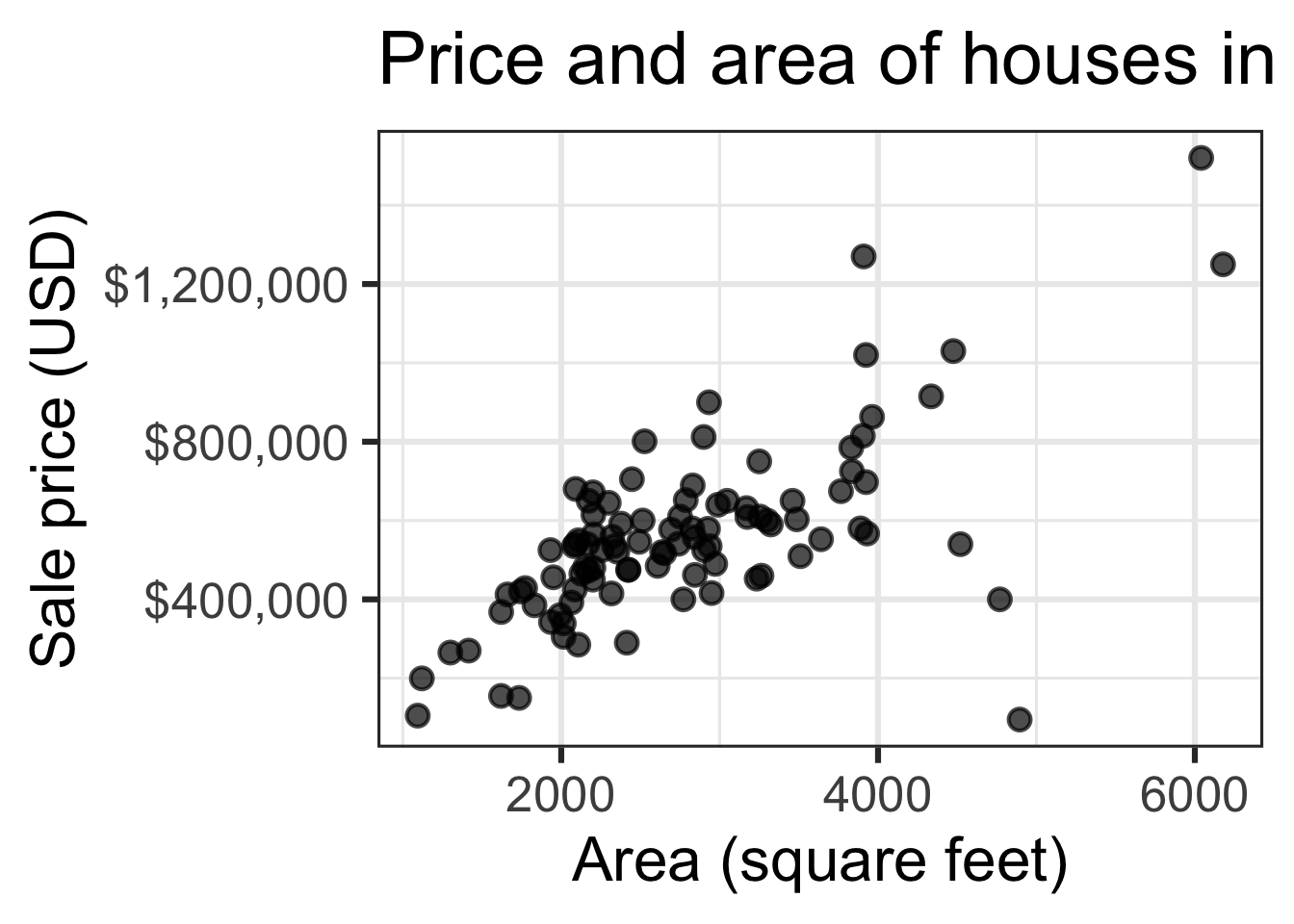
Data: Houses in Duke Forest
- Data on houses that were sold in the Duke Forest neighborhood of Durham, NC around November 2020
- Scraped from Zillow
- Source:
openintro::duke_forest
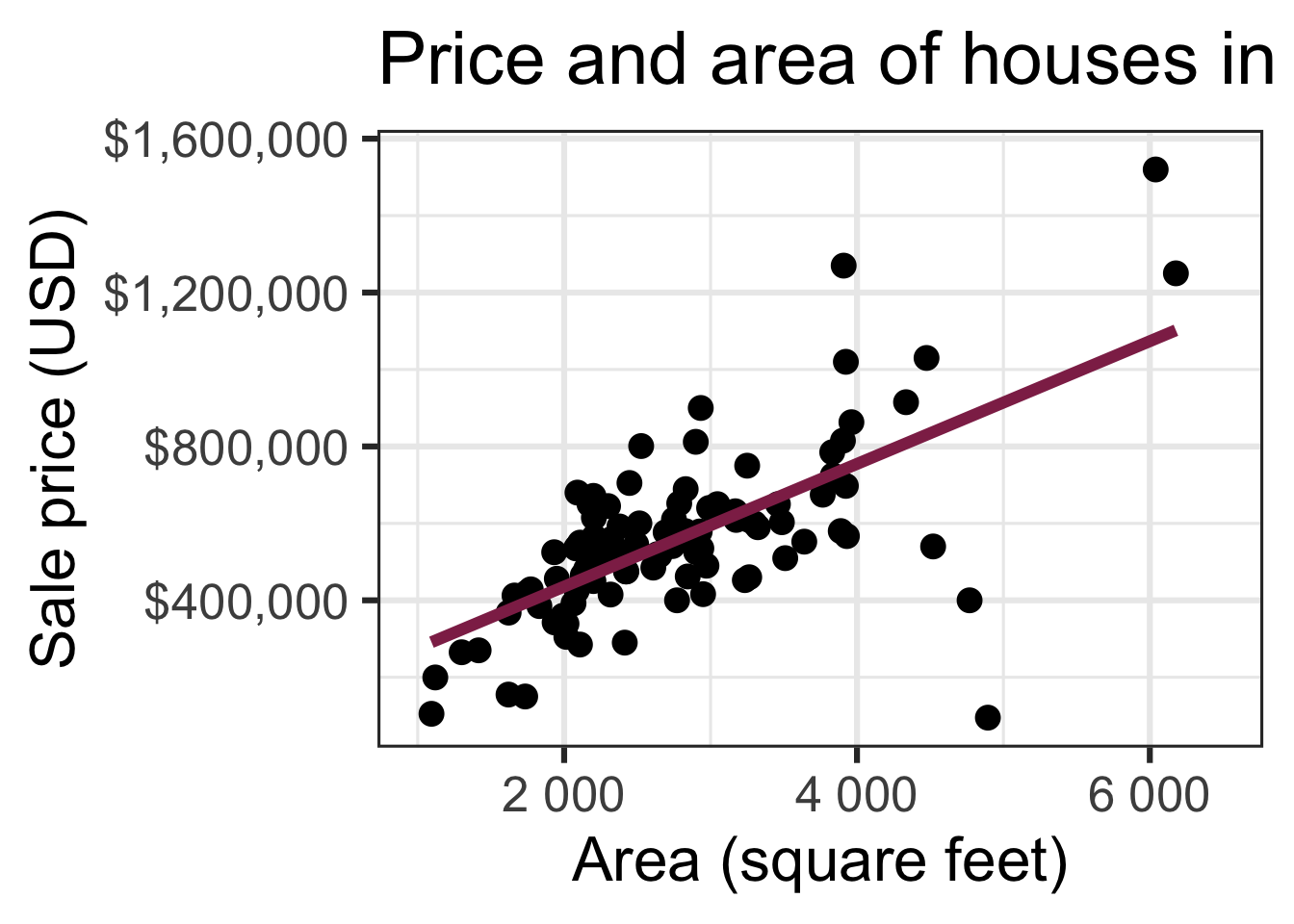
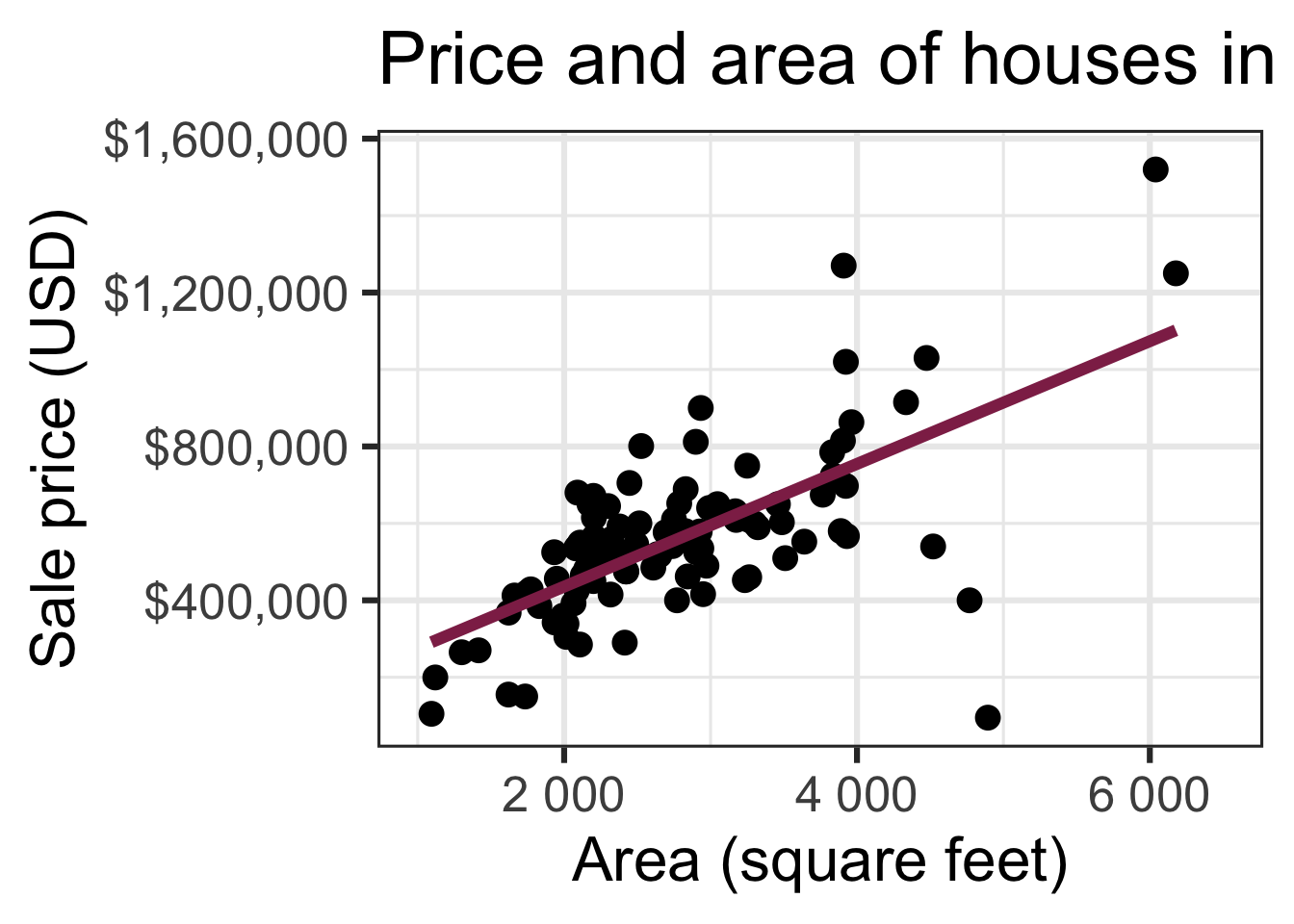
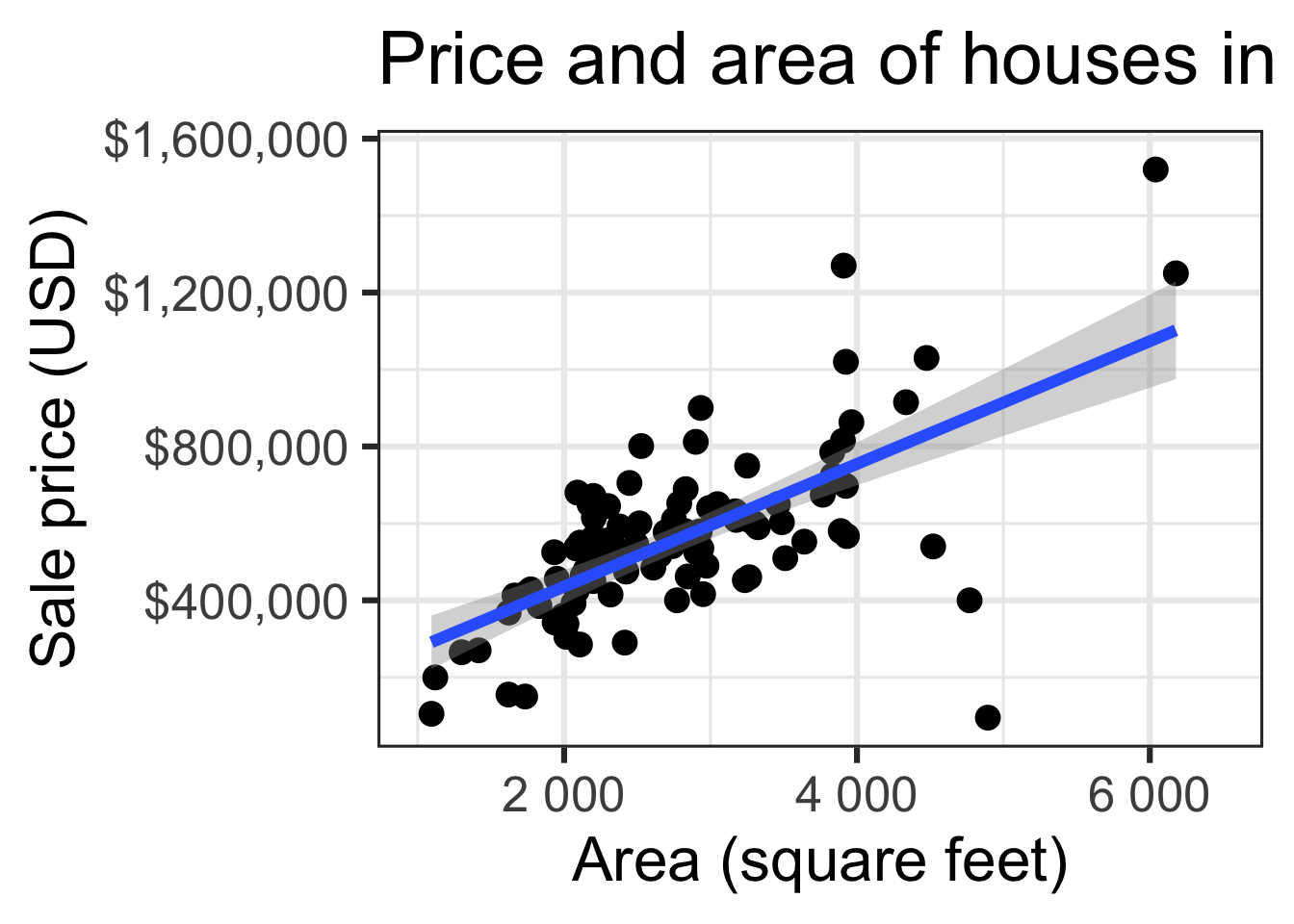
Goal: Use the area (in square feet) to understand variability in the price of houses in Duke Forest.
Exploratory data analysis
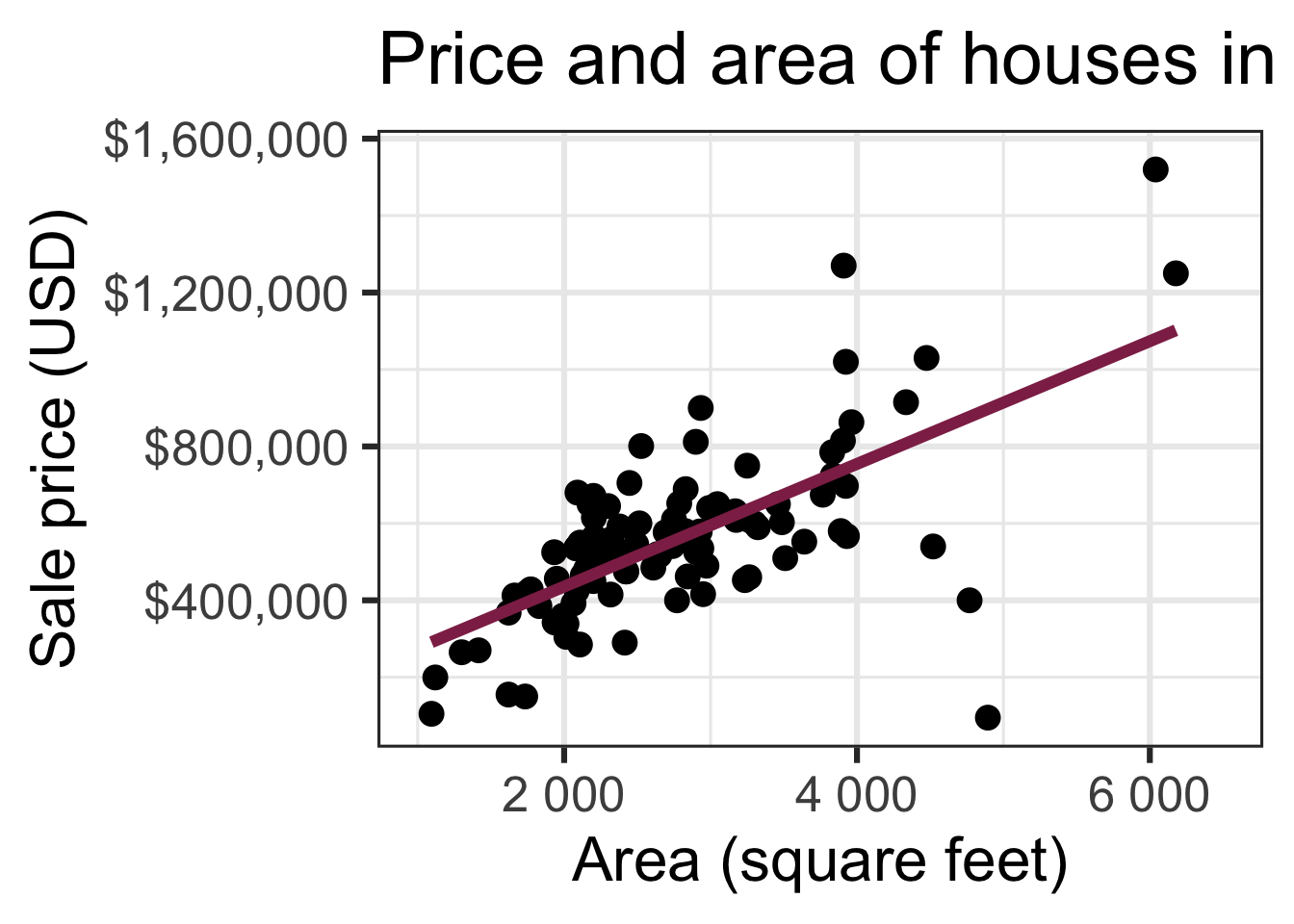
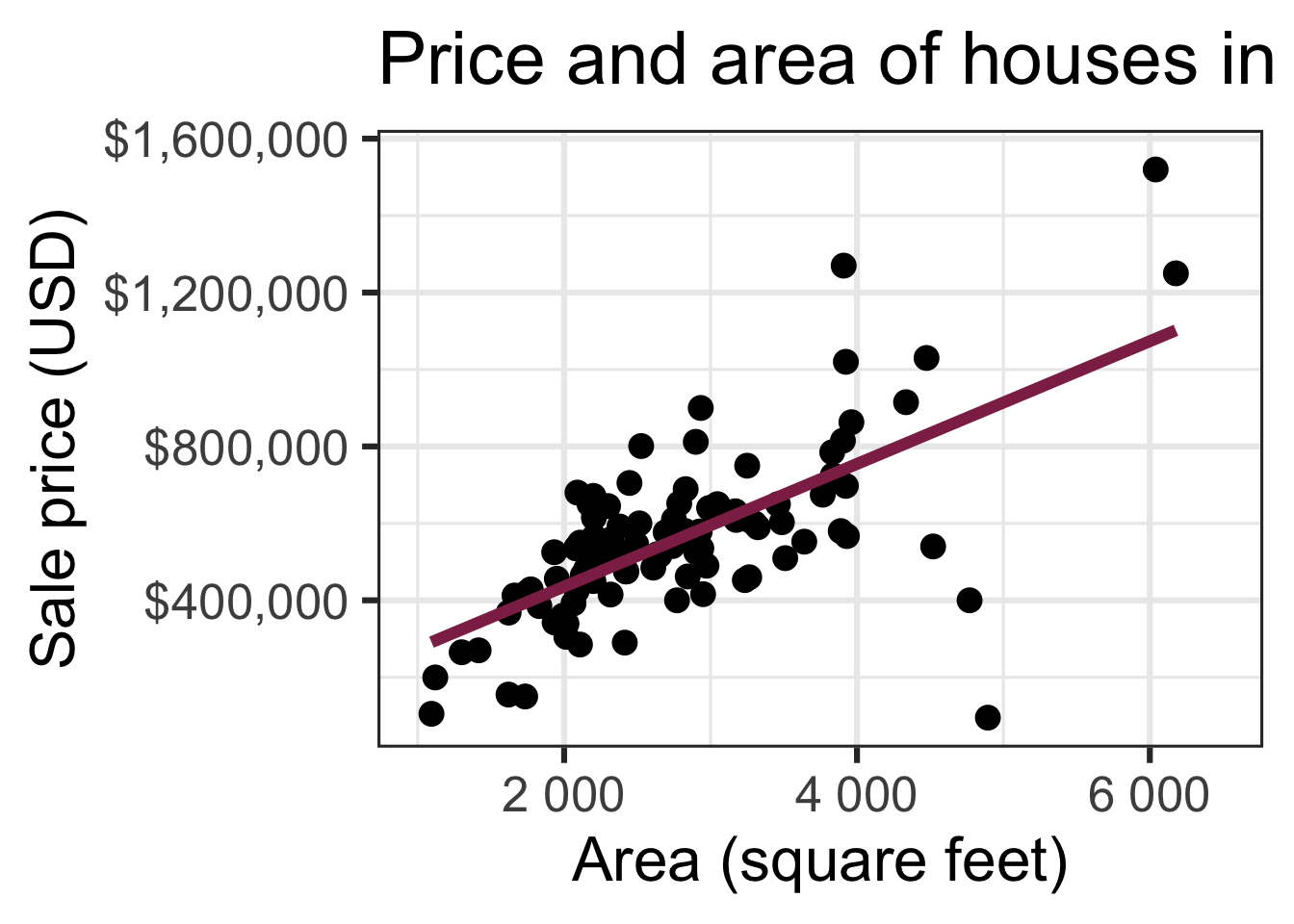
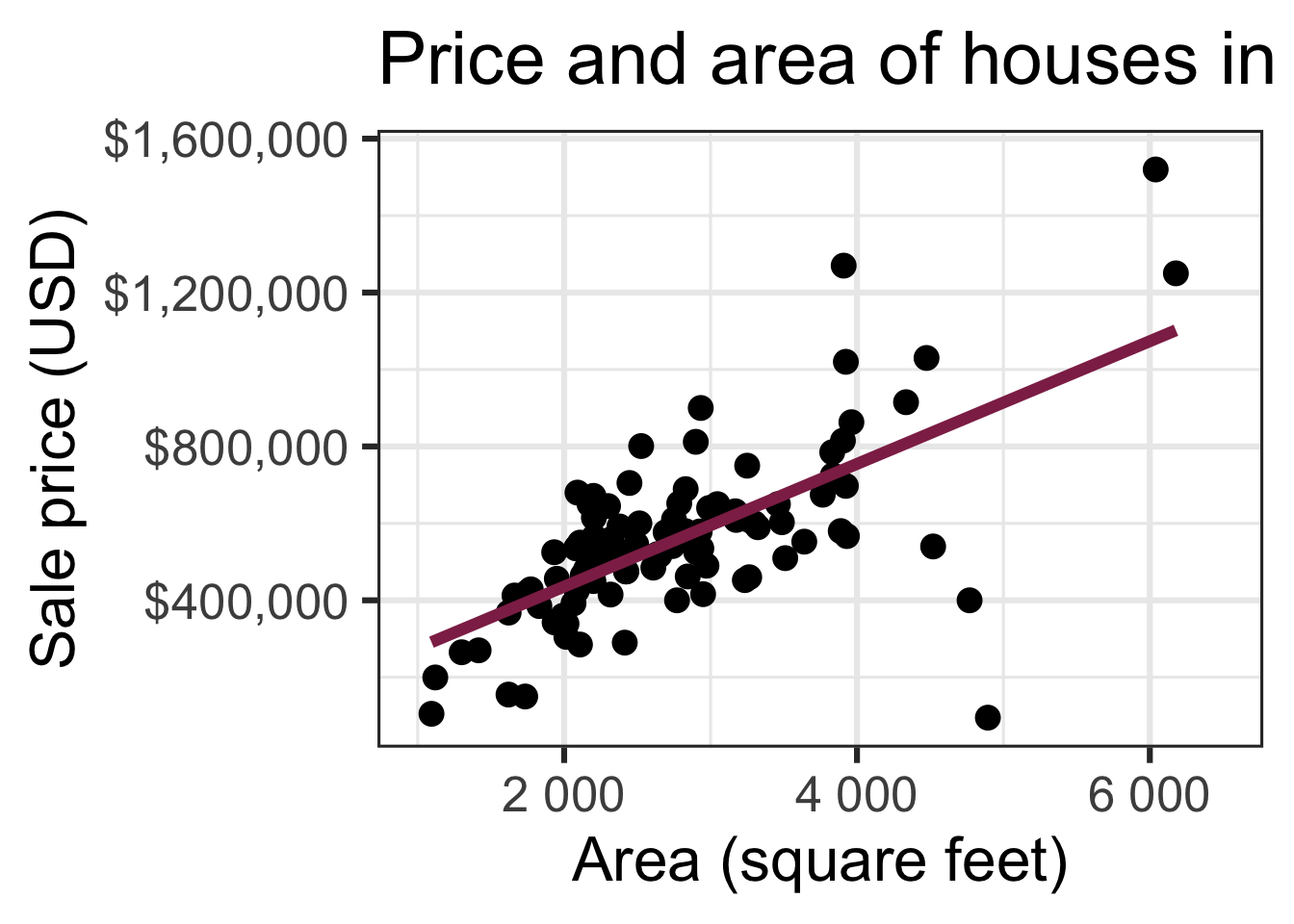
Code
ggplot(duke_forest, aes(x = area, y = price)) +
geom_point(alpha = 0.7) +
labs(
x = "Area (square feet)",
y = "Sale price (USD)",
title = "Price and area of houses in Duke Forest"
) +
scale_y_continuous(labels = label_dollar())Modeling
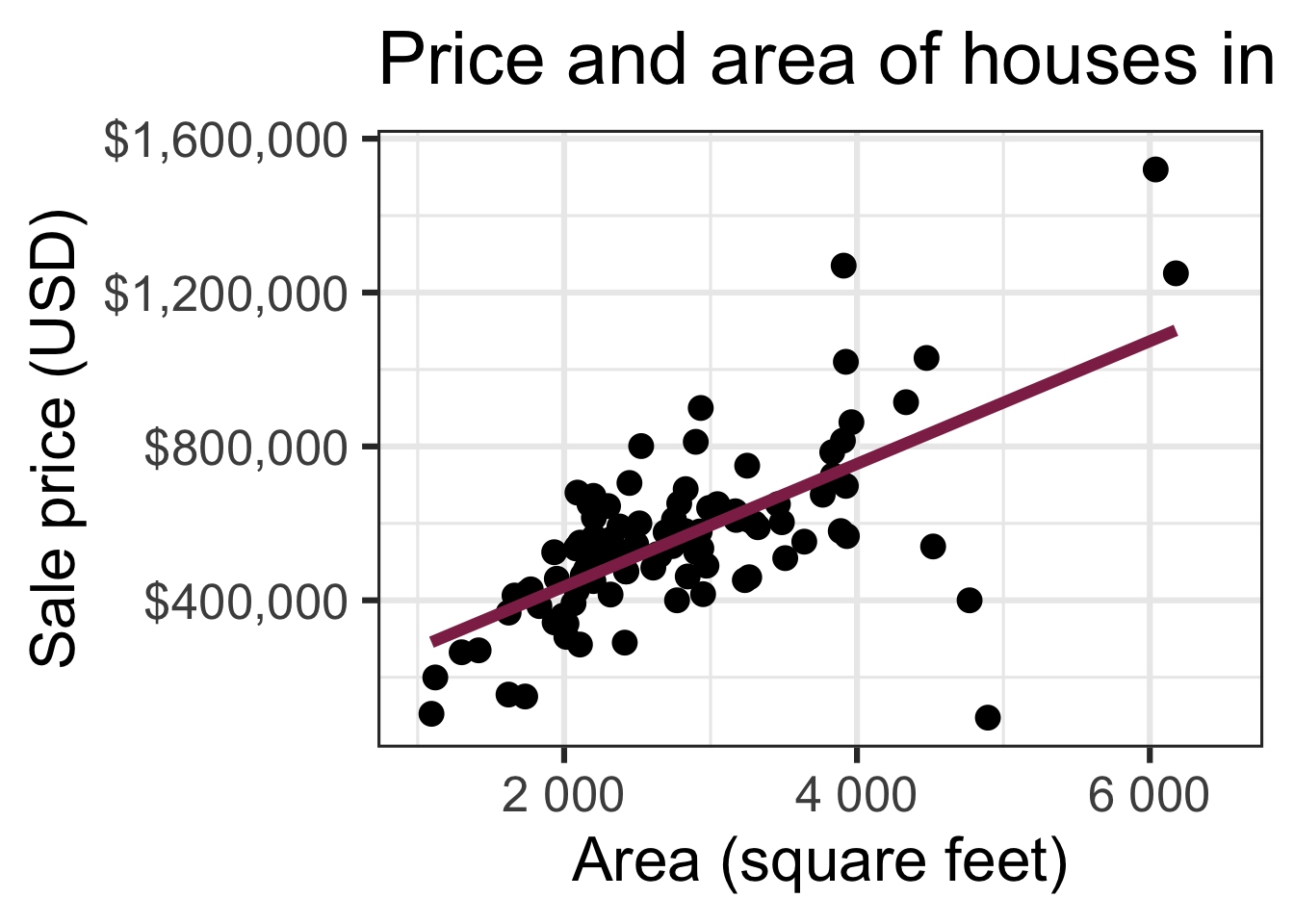
df_fit <- linear_reg() |>
fit(price ~ area, data = duke_forest)
tidy(df_fit) |>
kable(digits = 2) # neatly format table to 2 digits| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 116652.33 | 53302.46 | 2.19 | 0.03 |
| area | 159.48 | 18.17 | 8.78 | 0.00 |
Participate 📱💻
Which of the following is the correct interpretation of the intercept?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 116652 | 53302 | 2 | 0 |
| area | 159 | 18 | 9 | 0 |
- For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher by $116,652, on average.
- Duke Forest houses that are 0 square feet are predicted to sell, for $116,652, on average.
- For each additional square foot, the model predicts the sale price of Duke Forest houses to be lower by $15,900, on average.
- Duke Forest houses that are 0 square feet are predicted to sell, for $15,900, on average.
Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Participate 📱💻
Which of the following is the correct interpretation of the slope?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 116652 | 53302 | 2 | 0 |
| area | 159 | 18 | 9 | 0 |
- For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher by $159, on average.
- Duke Forest houses that are 0 square feet are predicted to sell, for $116,652, on average.
- For each additional square foot, the model predicts the sale price of Duke Forest houses to be lower by $15,900, on average.
- Duke Forest houses that are 0 square feet are predicted to sell, for $159, on average.
Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
From sample to population
For each additional square foot, we expect the sale price of Duke Forest houses to be higher by $159, on average.
- This estimate is valid for the single sample of 98 houses.
- But what if we’re not interested quantifying the relationship between the size and price of a house in this single sample?
- What if we want to say something about the relationship between these variables for all houses in Duke Forest?
Statistical inference
Statistical inference provide methods and tools so we can use the single observed sample to make valid statements (inferences) about the population it comes from
For our inferences to be valid, the sample should be random and representative of the population we’re interested in
Inference for simple linear regression
Calculate a confidence interval for the slope, \(\beta_1\) (today)
Conduct a hypothesis test for the slope,\(\beta_1\) (next week)
Confidence interval for the slope
Confidence interval
- A plausible range of values for a population parameter is called a confidence interval
- Using only a single point estimate is like fishing in a murky lake with a spear, and using a confidence interval is like fishing with a net
- We can throw a spear where we saw a fish but we will probably miss, if we toss a net in that area, we have a good chance of catching the fish
- Similarly, if we report a point estimate, we probably will not hit the exact population parameter, but if we report a range of plausible values we have a good shot at capturing the parameter
Confidence interval for the slope
A confidence interval will allow us to make a statement like “For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus X dollars.”
. . .
Should X be $10? $100? $1000?
If we were to take another sample of 98 would we expect the slope calculated based on that sample to be exactly $159? Off by $10? $100? $1000?
The answer depends on how variable (from one sample to another sample) the sample statistic (the slope) is
We need a way to quantify the variability of the sample statistic
Quantify the variability of the slope
for estimation
- Two approaches:
- Via simulation (what we’ll do in this course)
- Via mathematical models (what you can learn about in future courses)
-
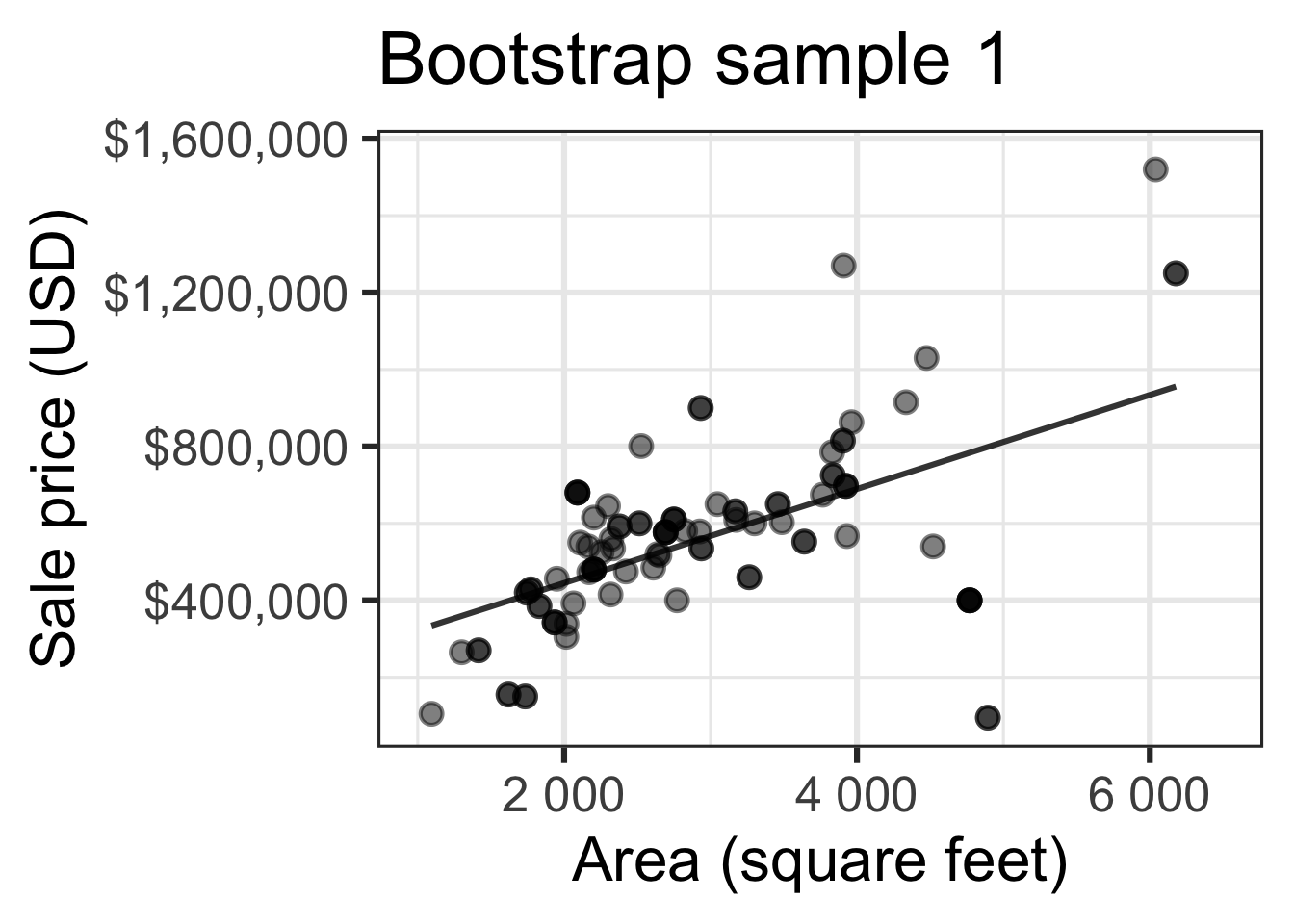
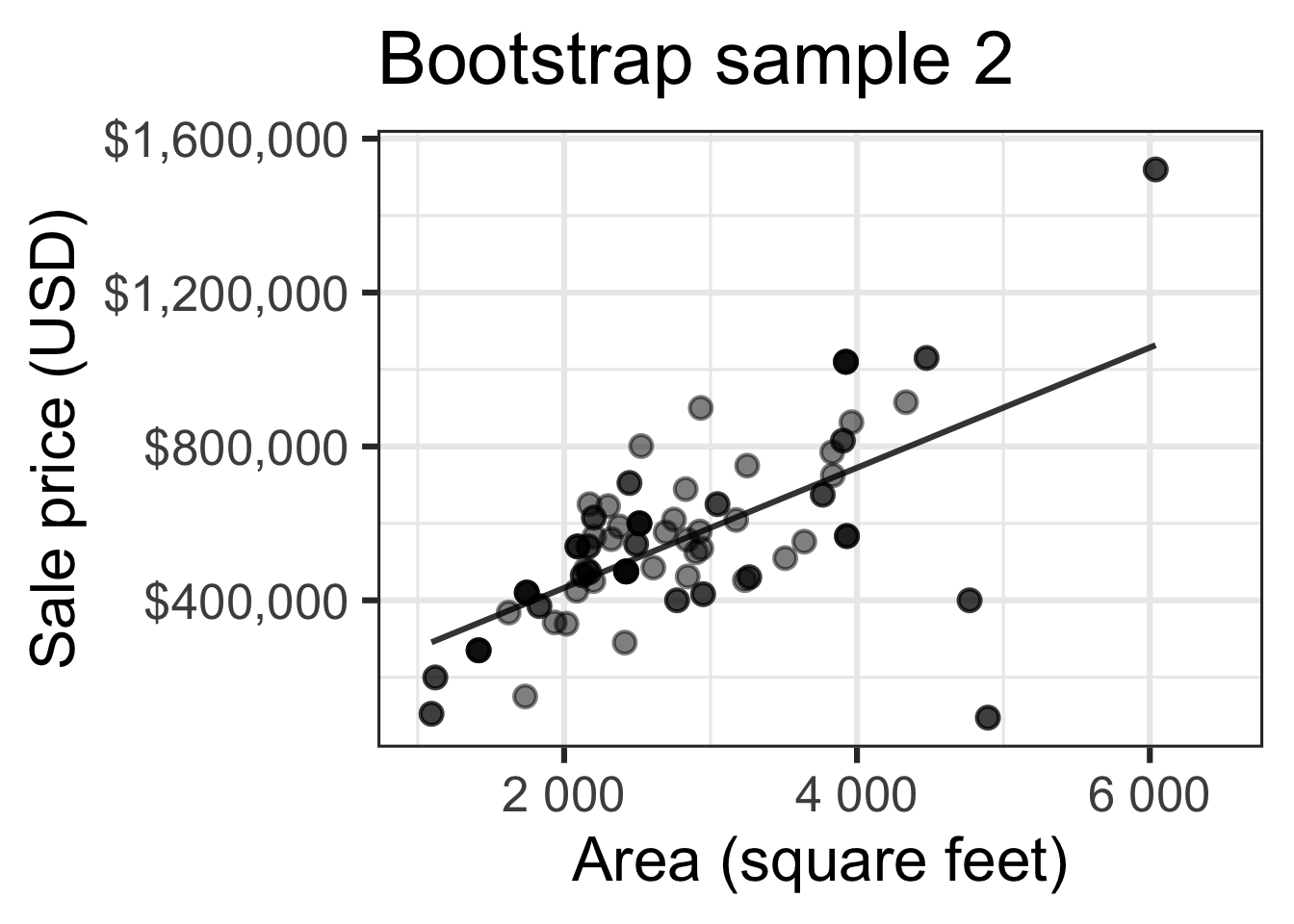
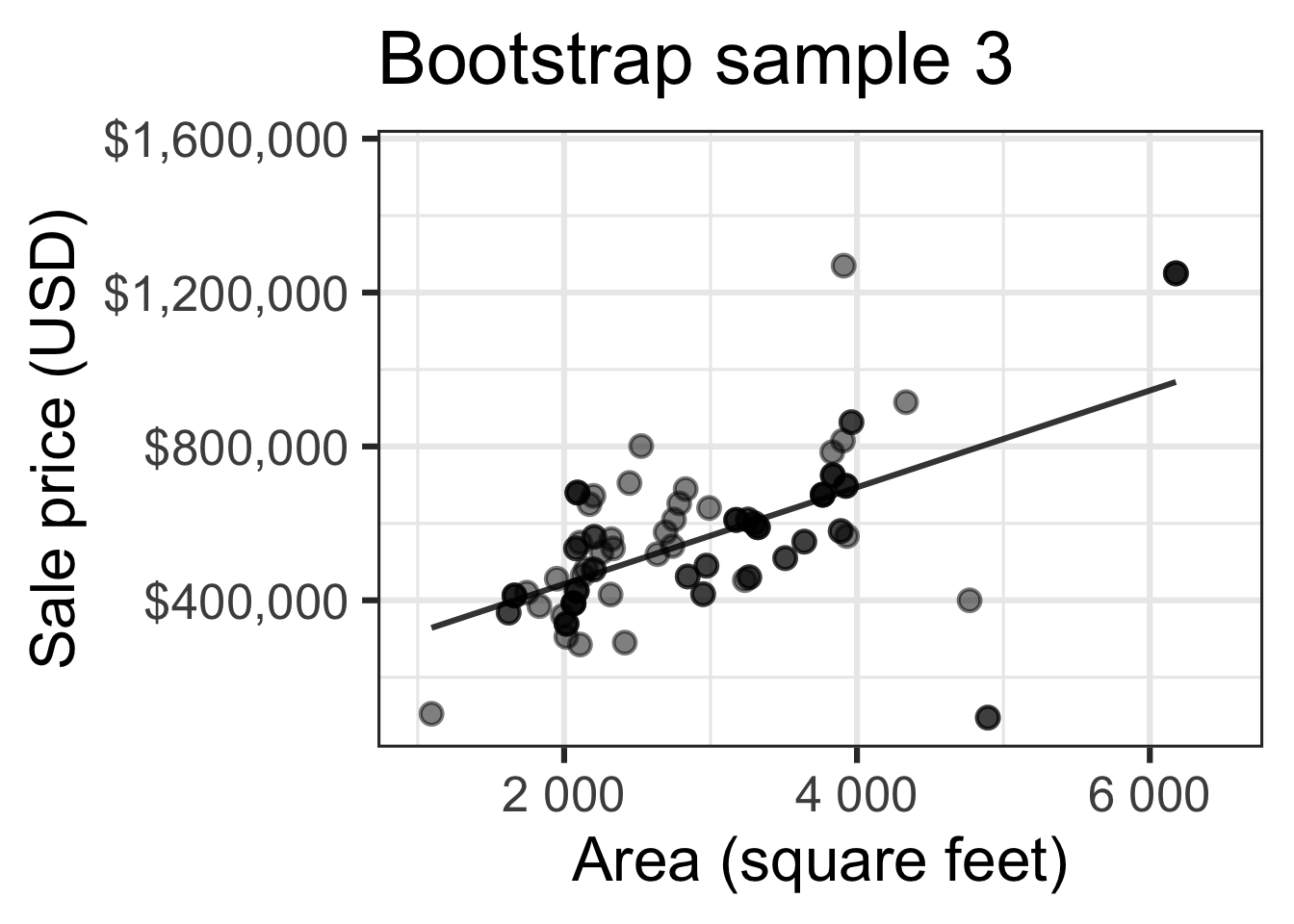
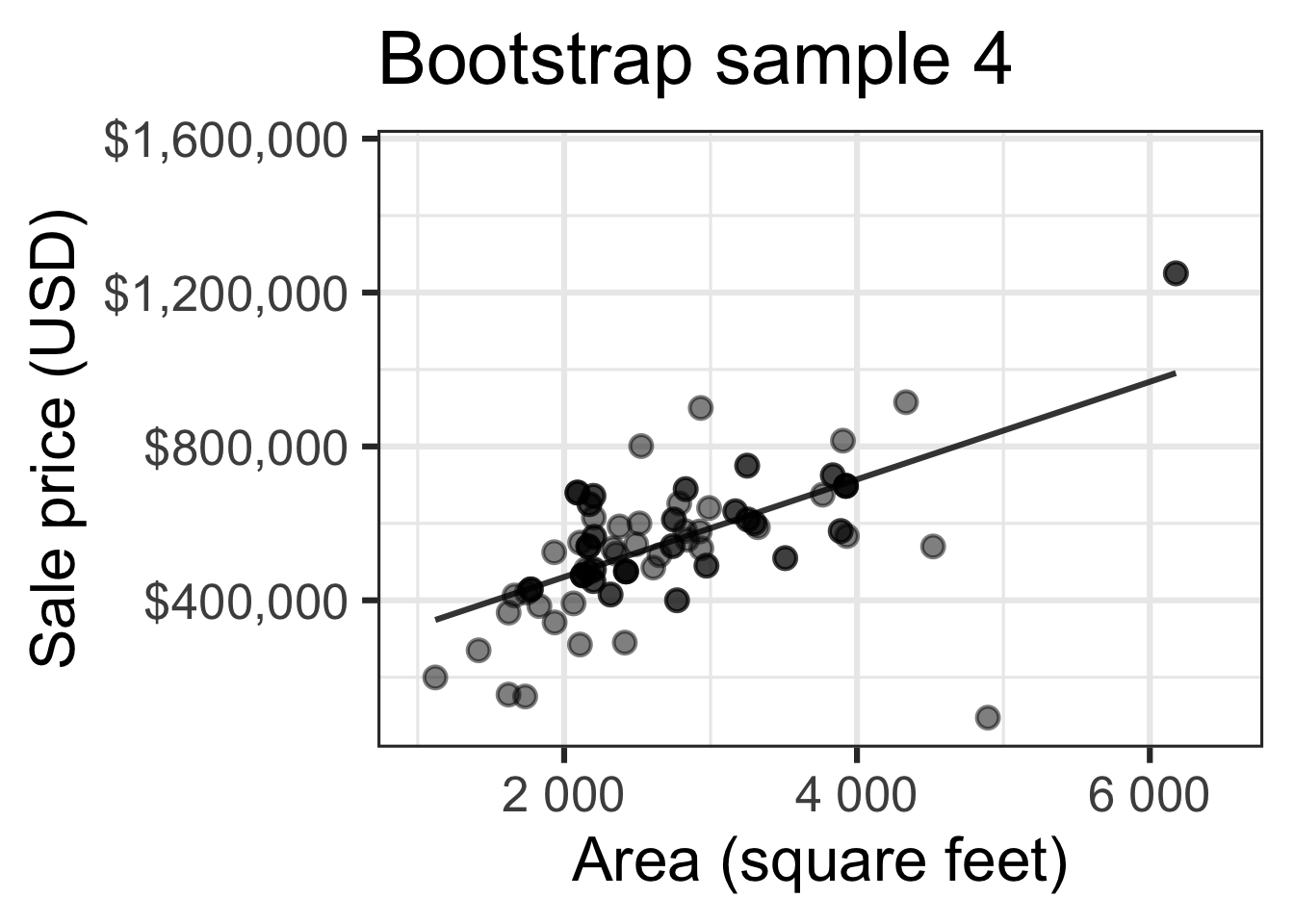
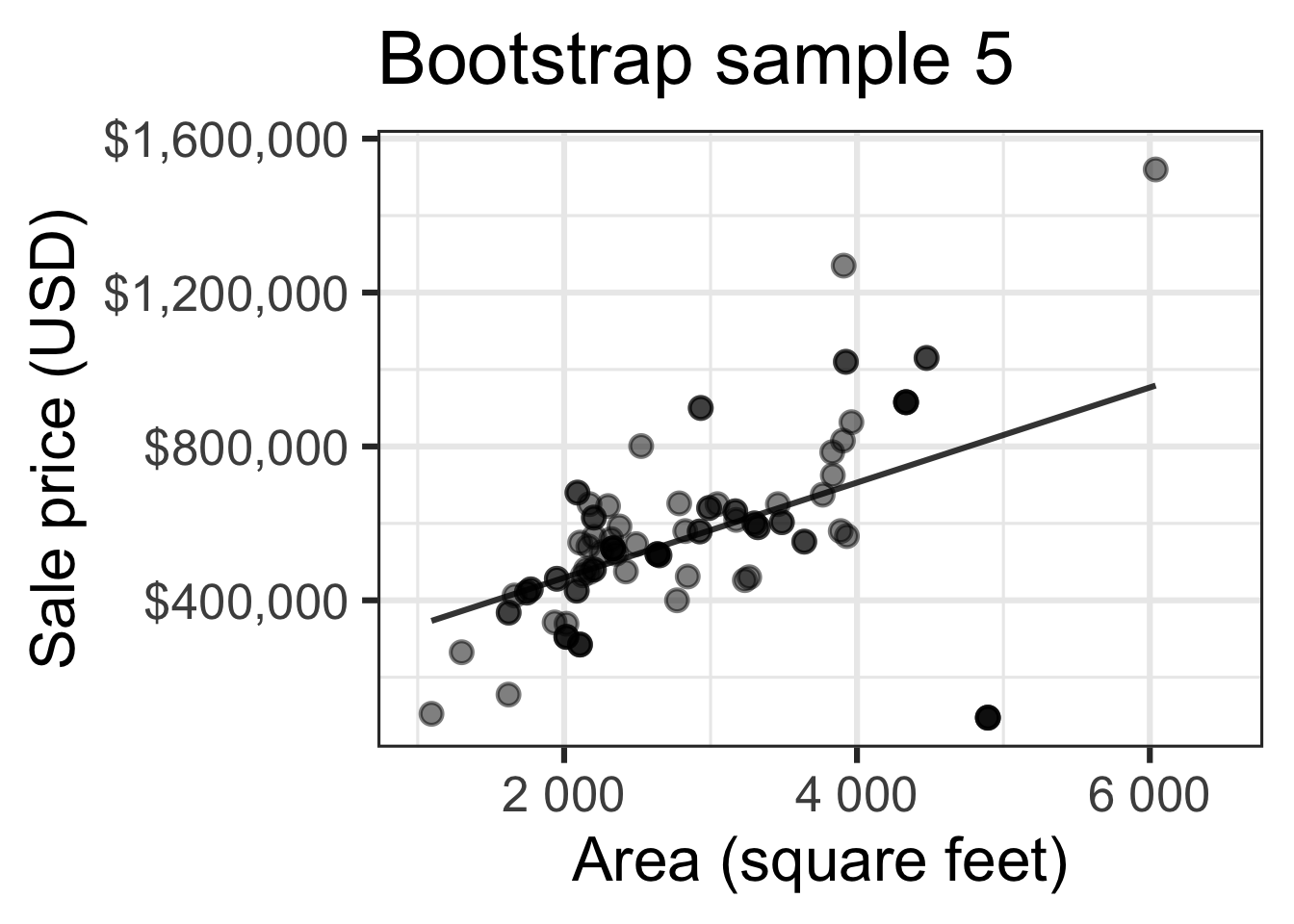
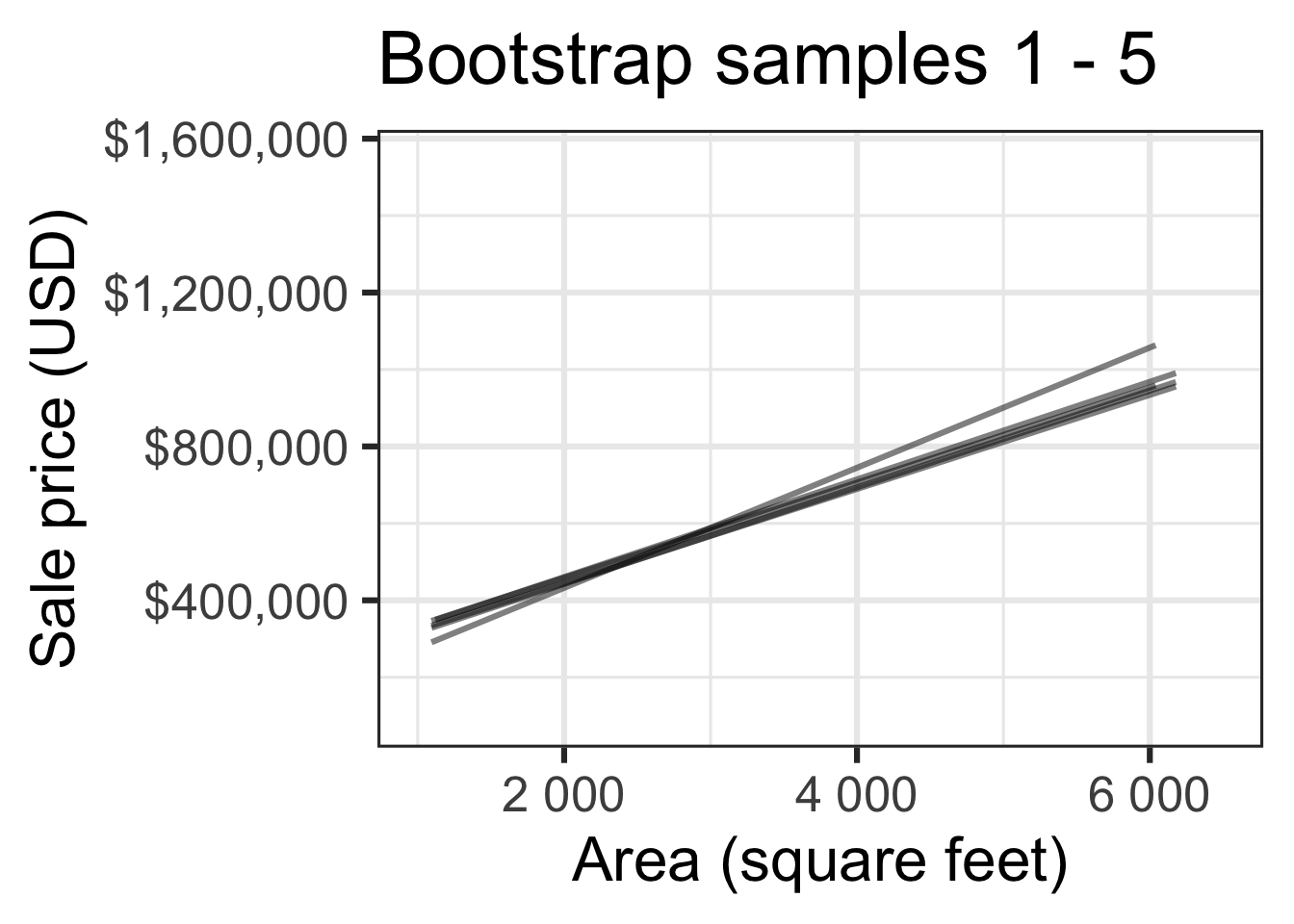
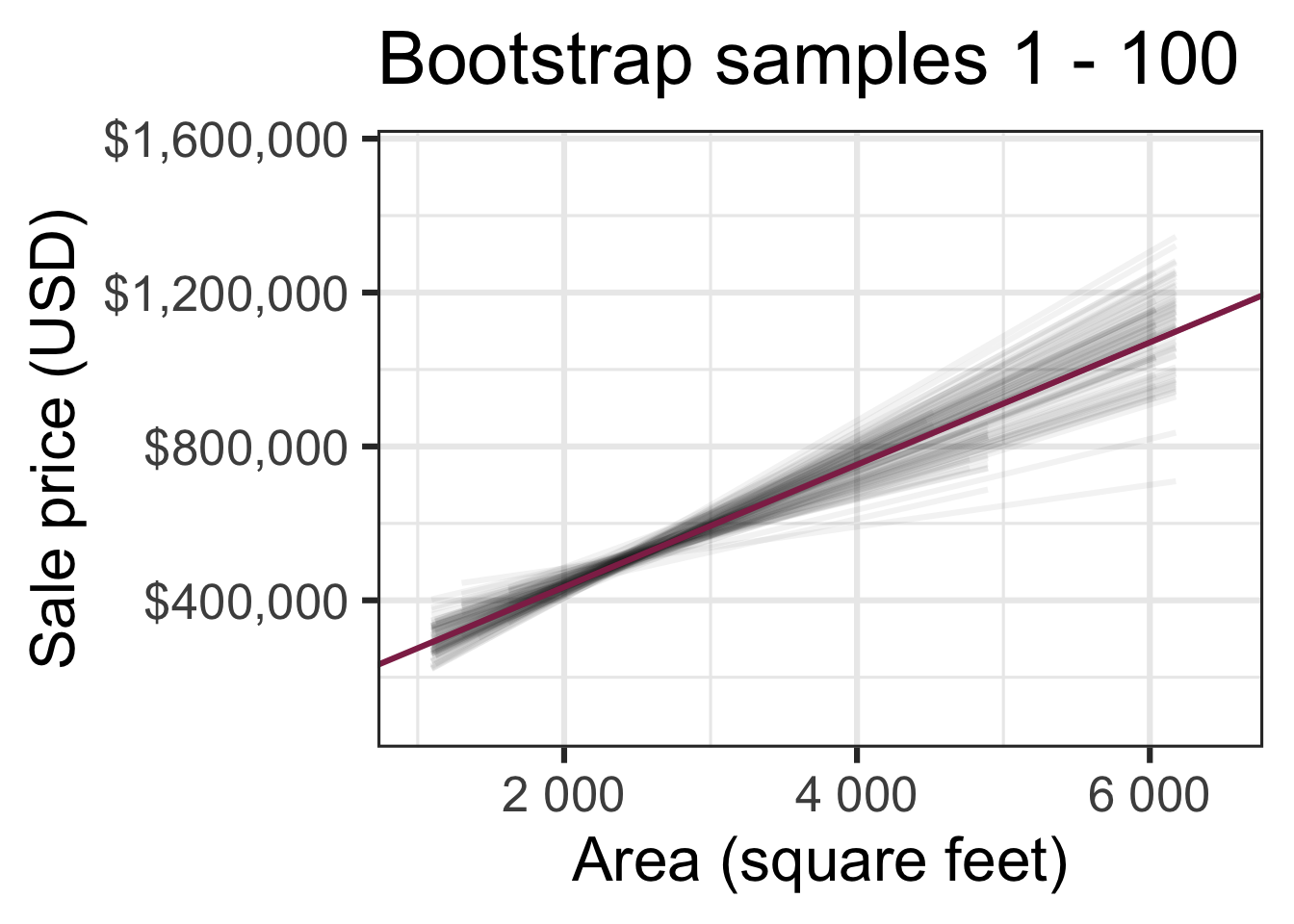
Bootstrapping to quantify the variability of the slope for the purpose of estimation:
- Bootstrap new samples from the original sample
- Fit models to each of the samples and estimate the slope
- Use features of the distribution of the bootstrapped slopes to construct a confidence interval
Bootstrap sample 1
Bootstrap sample 2
Bootstrap sample 3
Bootstrap sample 4
Bootstrap sample 5
. . .
so on and so forth…
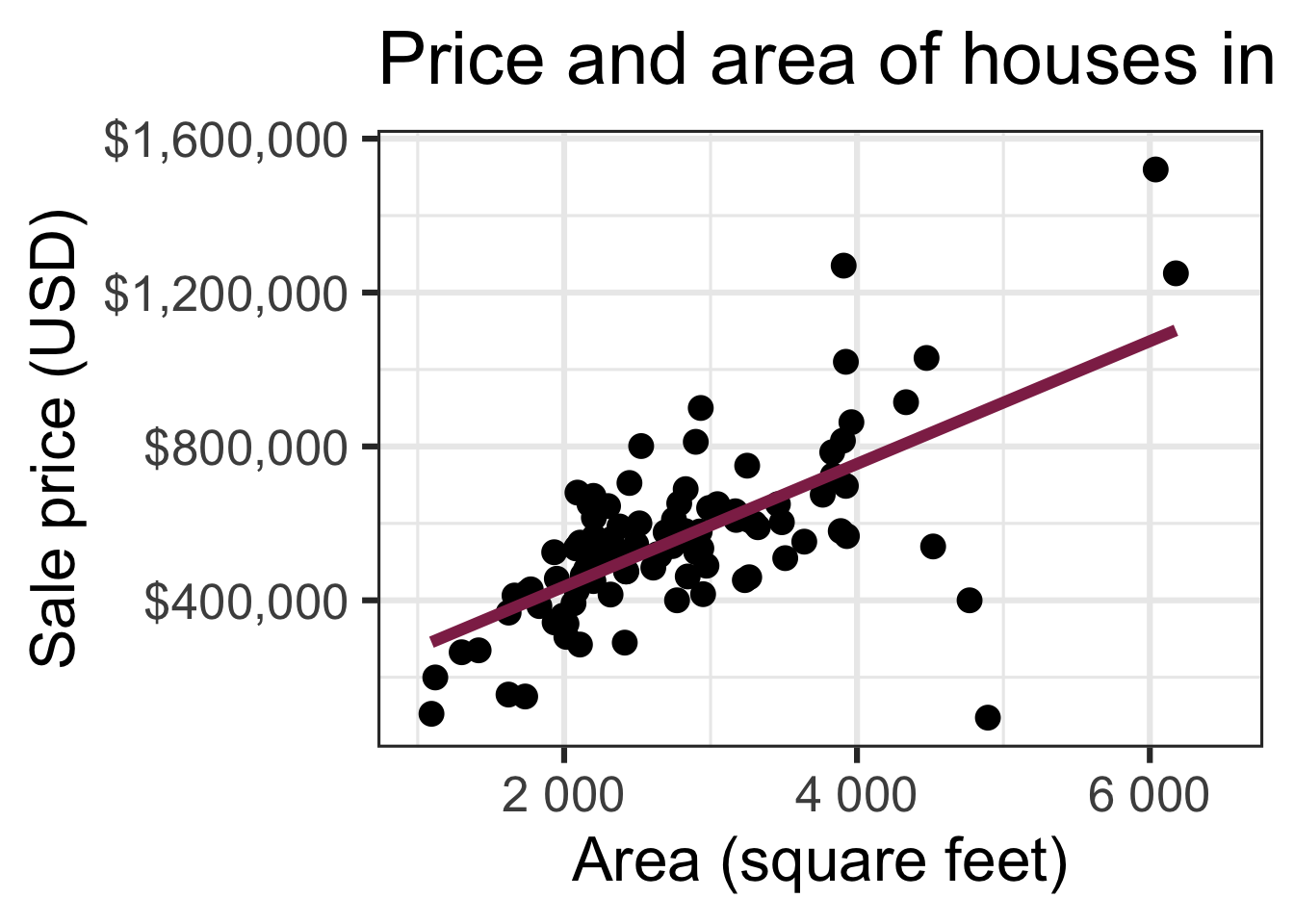
Bootstrap samples 1 - 5
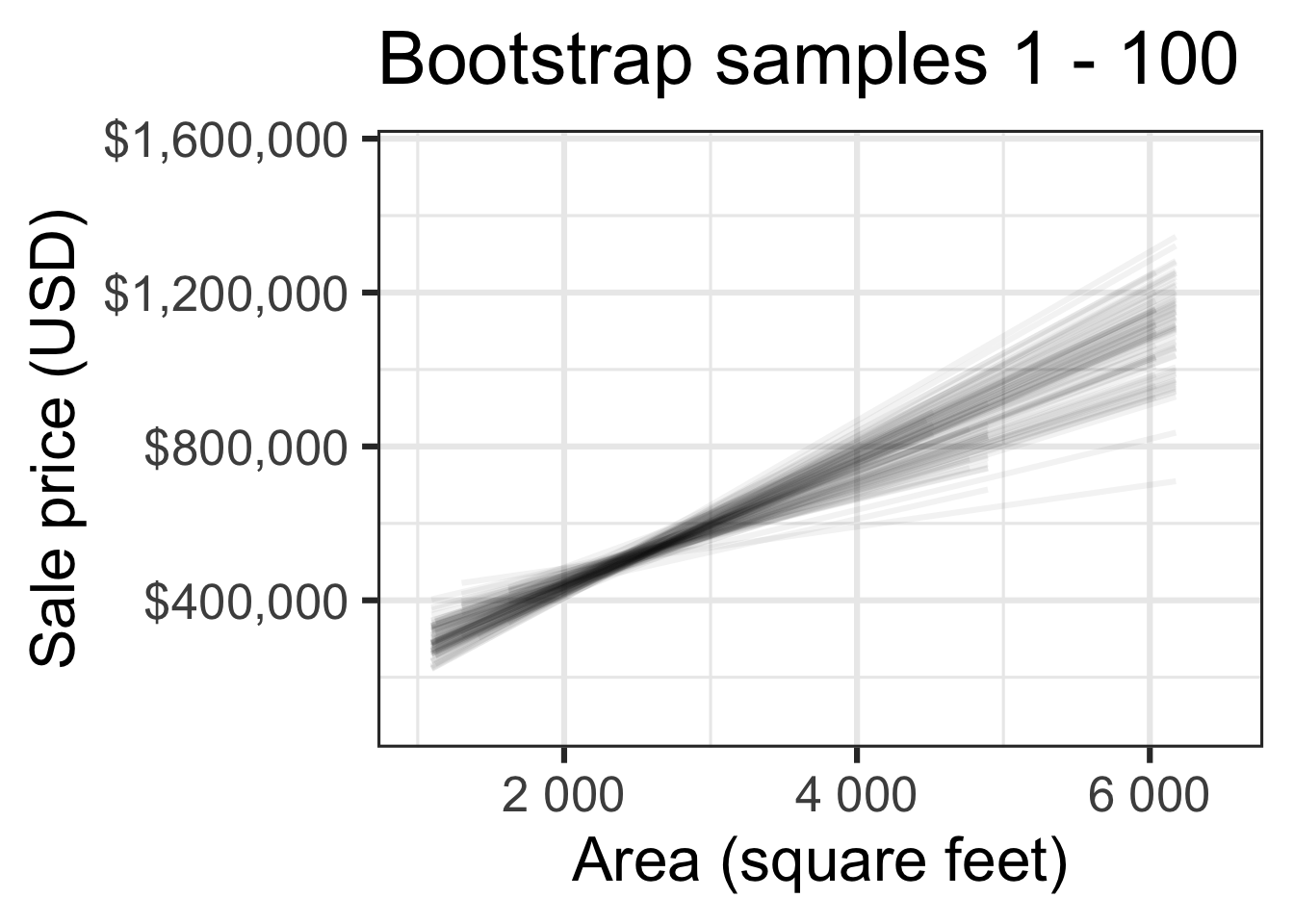
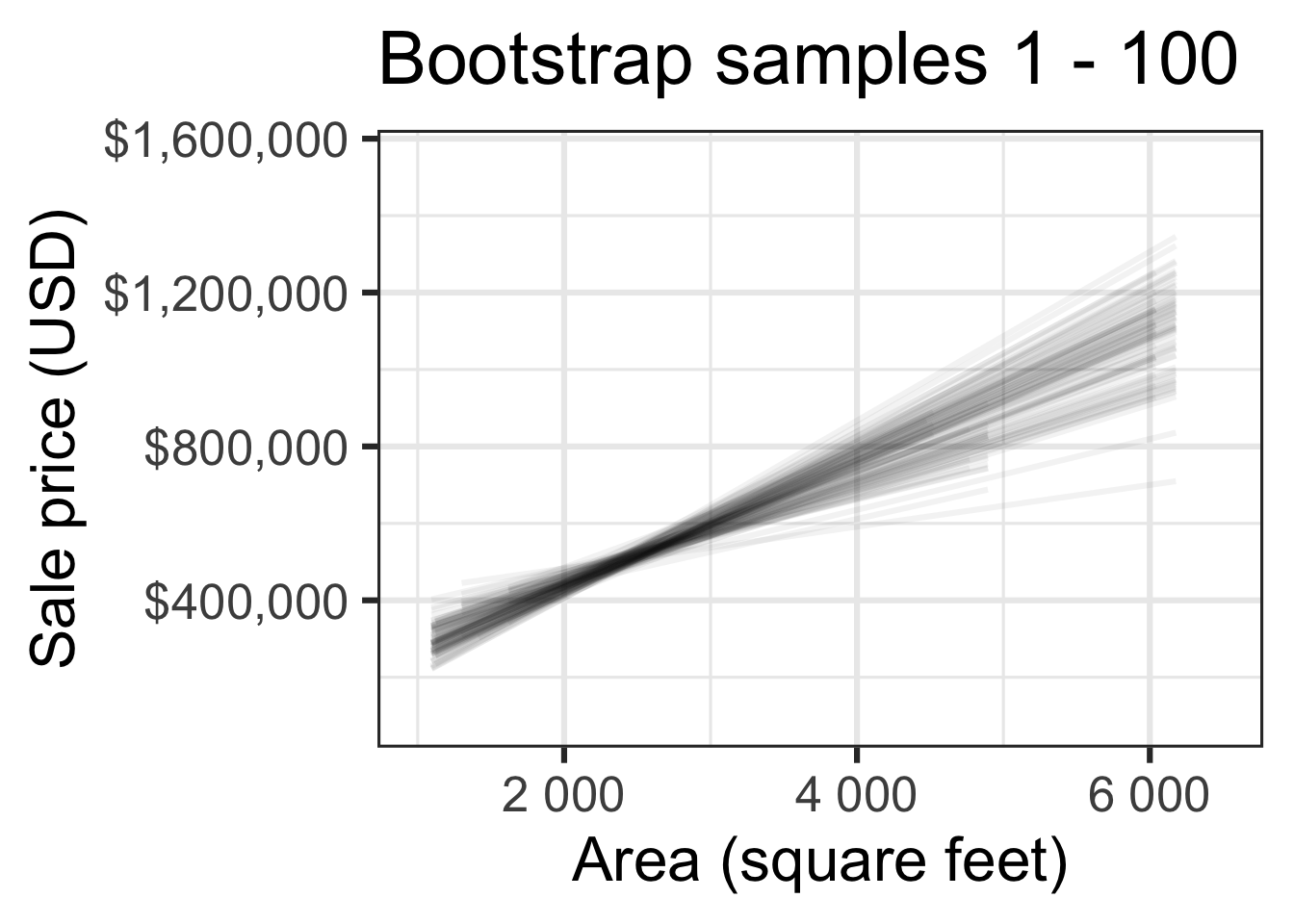
Bootstrap samples 1 - 100
. . .
Look familiar?
Look familiar?
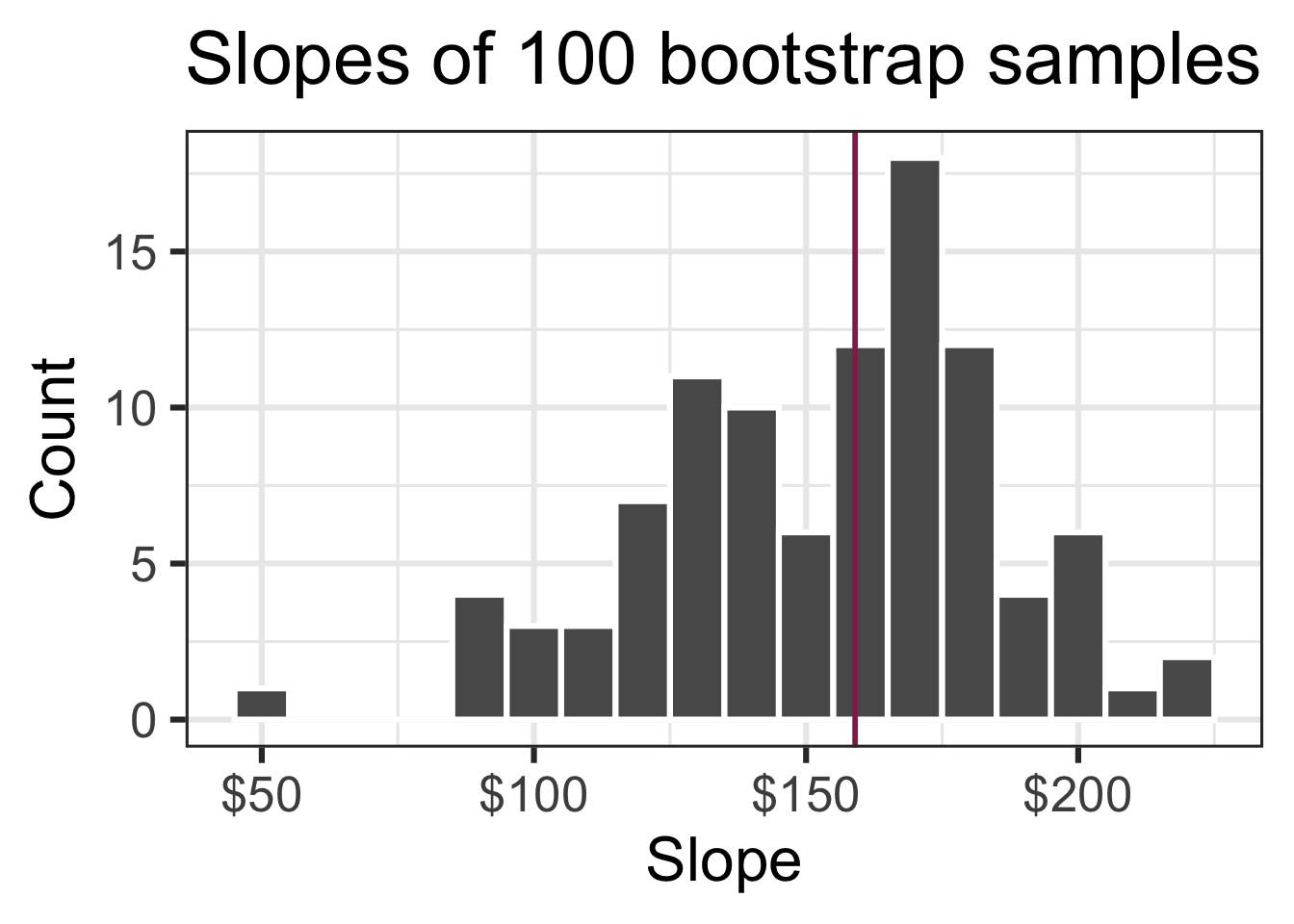
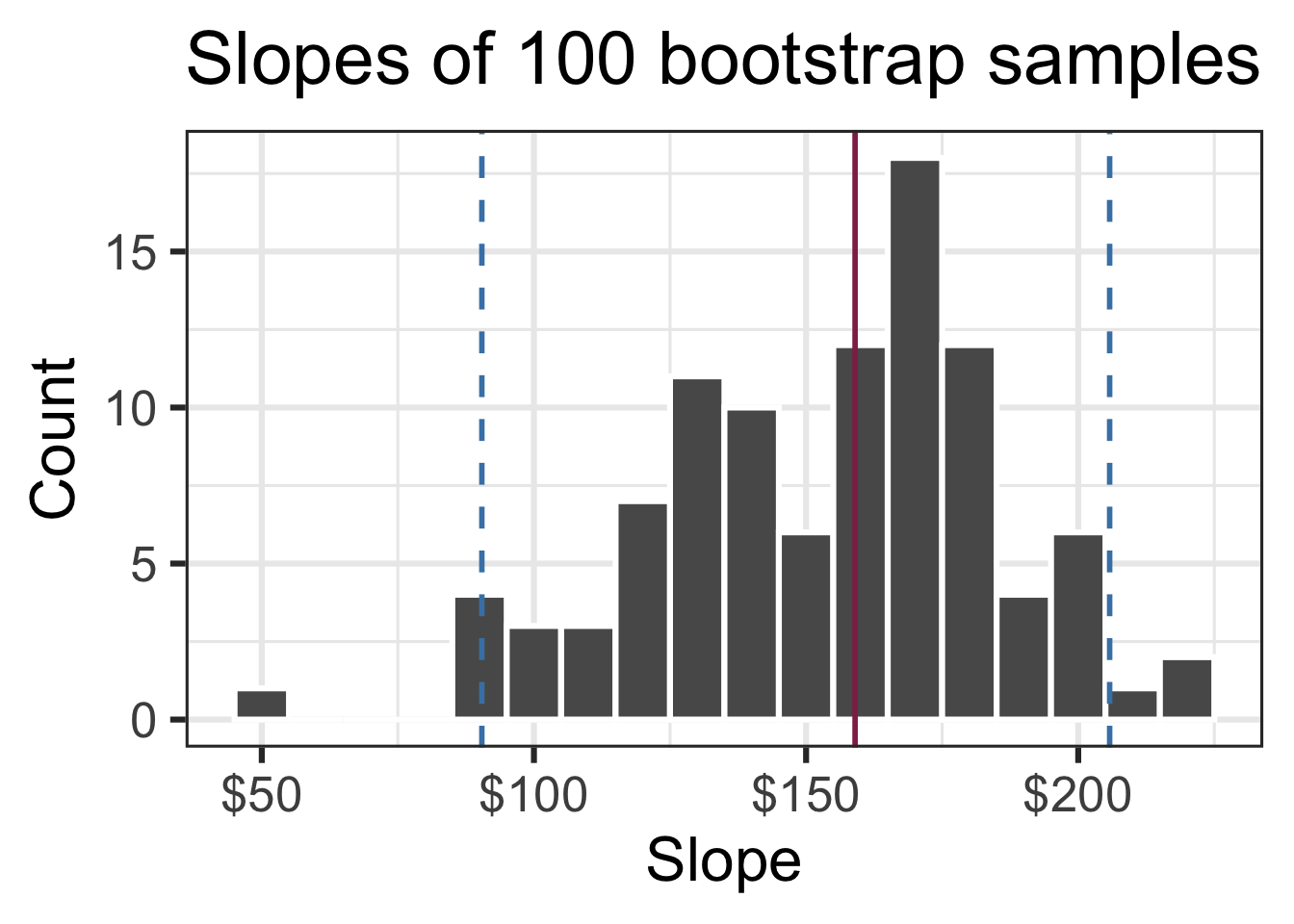
Slopes of bootstrap samples
Fill in the blank: For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus ___ dollars.
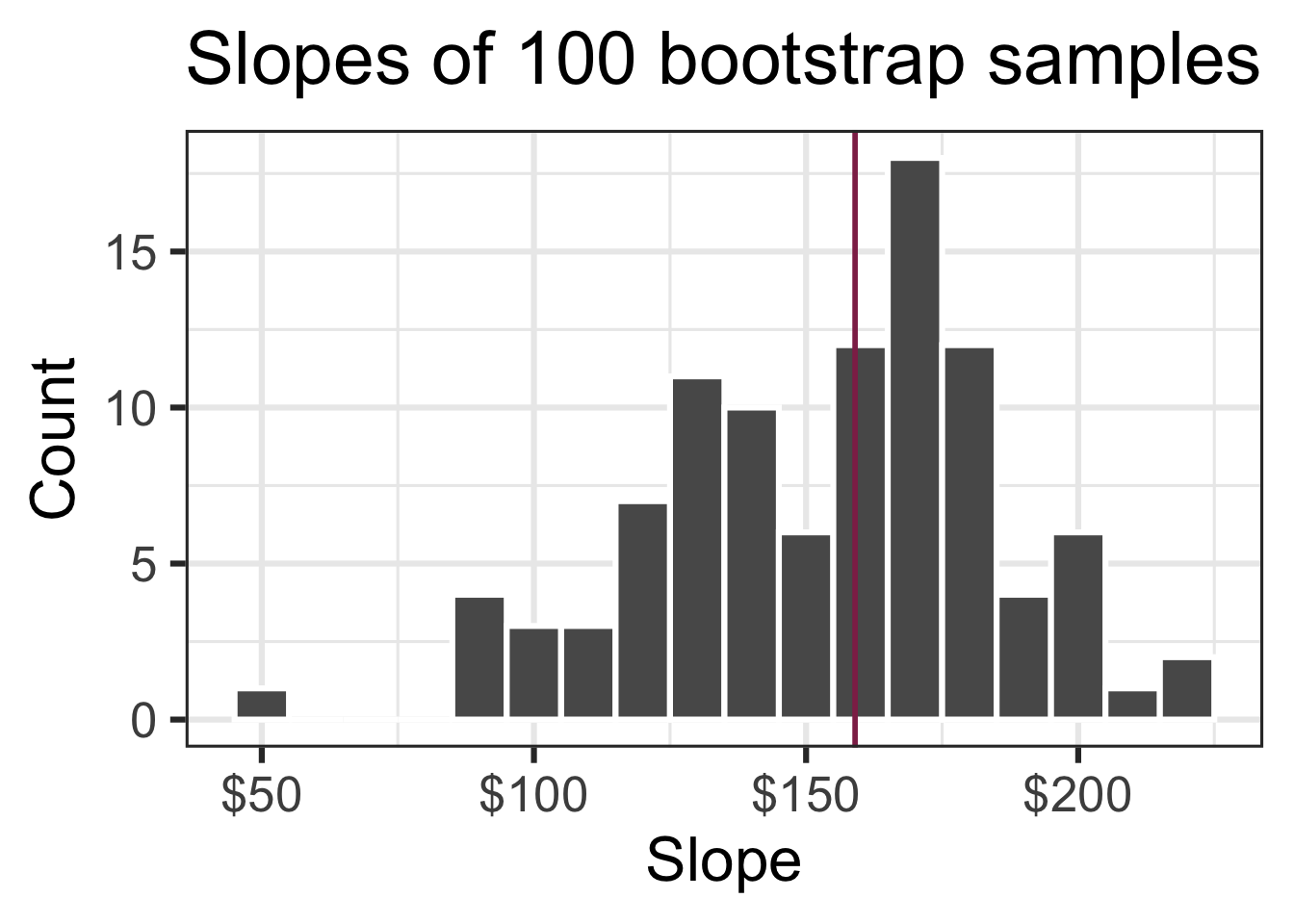
Slopes of bootstrap samples
Fill in the blank: For each additional square foot, we expect the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus ___ dollars.
Confidence level
How confident are you that the true slope is between $0 and $250? How about $150 and $170? How about $90 and $210?
95% confidence interval
- A 95% confidence interval is bounded by the middle 95% of the bootstrap distribution
- We are 95% confident that for each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $90.43 to $205.77.
Application exercise
ae-15-duke-forest-bootstrap
Go to your ae project in RStudio.
If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
If you haven’t yet done so, click Pull to get today’s application exercise file: ae-15-duke-forest-bootstrap.qmd.
Work through the application exercise in class, and render, commit, and push your edits.