Exam 2 review
Lecture 23
Duke University
STA 199 - Fall 2025
November 18, 2025
Warm-up
Announcements
-
Exam - In class:
- Cheat sheet: 8.5x11, both sides, hand written or typed, any content you want, must be prepared by you
- Bring a pencil and eraser (you’re allowed to use a pen, but you might not want to)
-
Exam - Take home:
- Open book, notes, internet
- No office hours
- Questions on Ed (private by default)
- Due Saturday, November 22 at noon
Reminder: Academic dishonesty / Duke Community Standard
Next Tuesday: Can watch class live on Panopto link
From last class: ae-14-chicago-taxi-classification
Finish up the application exercise by finding the area under the ROC curve.
Recap
Split data into training and testing sets (generally 75/25)
Fit models on training data and reduce to a few candidate models
Make predictions on testing data
-
Evaluate predictions on testing data using appropriate predictive performance metrics
- Linear models: Adjusted R-squared, AIC, etc.
- Logistic models: False negative and positive rates, AUC (area under the curve), etc.
Don’t forget to also consider explainability and domain knowledge when selecting a final model
In a future machine learning course: Cross-validation (partitioning training data into training and validation sets and repeating this many times to evaluate model predictive performance before using the testing data), feature engineering, hyperparameter tuning, more complex models (random forests, gradient boosting machines, neural networks, etc.)
Modeling review
Hotel cancellations
Data prep
- Relevel
is_canceled - Remove bookings with average daily rate greater than $1,000
- Remove bookings with number of adults greater than or equal to 5
- Split the data into a training set (75%) and a testing set (25%)
hotels <- hotels |>
mutate(
is_canceled = if_else(is_canceled == 1, "canceled", "not canceled"),
is_canceled = fct_relevel(is_canceled, "not canceled", "canceled")
) |>
filter(adr <= 1000, adults < 5)
set.seed(1117)
hotels_split <- initial_split(hotels)
hotels_train <- training(hotels_split)
hotels_test <- testing(hotels_split)Participate 📱💻
What type of model would you use to answer the question:
Are reservations earlier in the month or later in the month more likely to be cancelled?
- Linear regression with a numerical predictor
- Linear regression with a categorical predictor
- Linear regression with a log-transformed outcome and a numerical predictor
- Linear regression with a log-transformed outcome and a categorical predictor
- Logistic regression with a numerical predictor ✅
- Logistic regression with a categorical predictor

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Linear regression
Numerical outcome:
\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \varepsilon \]
\[ \widehat{y} = b_0 + b_1 x_1 + b_2 x_2 + \cdots + b_k x_k \]
Linear regression with log-transformed outcome
Numerical outcome, log-transformed for a better linear fit:
\[ log(y) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \varepsilon \]
\[ log(\widehat{y}) = b_0 + b_1 x_1 + b_2 x_2 + \cdots + b_k x_k \]
Logistic regression
Binary outcome, where \(p = P(Y=1)\), the probability of success:
\[ \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \varepsilon \]
\[ \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) = b_0 + b_1 x_1 + b_2 x_2 + \cdots + b_k x_k \]
Cancellation ~ arrival date
is_canceled_fit_1 <- logistic_reg() |>
fit(is_canceled ~ arrival_date_day_of_month, data = hotels_train)
tidy(is_canceled_fit_1)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -0.510 0.0142 -35.8 1.80e-280
2 arrival_date_day_of_month -0.00152 0.000789 -1.93 5.41e- 2Slope in logistic regression
# A tibble: 2 × 3
term estimate exp_estimate
<chr> <dbl> <dbl>
1 (Intercept) -0.510 0.601
2 arrival_date_day_of_month -0.00152 0.998For each day the booking is later in the month, the odds of reservations being canceled is predicted to be lower by a factor of 0.998, on average.
Intercept in logistic regression
# A tibble: 2 × 3
term estimate exp_estimate
<chr> <dbl> <dbl>
1 (Intercept) -0.510 0.601
2 arrival_date_day_of_month -0.00152 0.998On the 0th day of the month, the odds of reservations being canceled is predicted to be 0.601, on average. The intercept is not meaningful in this context since there is no 0th day of the month.
Prediction in logistic regression
Predict the probability of cancellation for a booking made on the 18th day of the month.
augment() vs. predict()
-
augment()returns the data frame passed tonew_data_augment_ed by- the predicted probability of success,
- the predicted probability of failure, and
- the predicted class (based on a 0.5 cutoff by default)
# A tibble: 1 × 4
.pred_class `.pred_not canceled` .pred_canceled
<fct> <dbl> <dbl>
1 not canceled 0.631 0.369
# ℹ 1 more variable: arrival_date_day_of_month <dbl>-
predict()the predicted class (based on a 0.5 cutoff by default)
Cancellation ~ arrival date + hotel type
Fit another model to predict whether a reservation was cancelled from arrival_date_day_of_month and hotel type (Resort or City Hotel), allowing the relationship between arrival_date_day_of_month and is_canceled to not vary based on hotel type.
is_canceled_fit_2 <- logistic_reg() |>
fit(is_canceled ~ arrival_date_day_of_month + hotel, data = hotels_train)
tidy(is_canceled_fit_2)# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -0.315 0.0151 -20.9 3.46e-97
2 arrival_date_day_of_month -0.00155 0.000797 -1.94 5.18e- 2
3 hotelResort Hotel -0.614 0.0153 -40.0 0 Slope in logistic regression
# A tibble: 3 × 3
term estimate exp_estimate
<chr> <dbl> <dbl>
1 (Intercept) -0.315 0.729
2 arrival_date_day_of_month -0.00155 0.998
3 hotelResort Hotel -0.614 0.541Holding hotel type constant, for each day the booking is later in the month, the odds of reservations being canceled is predicted to be lower by a factor of 0.998, on average.
Slope in logistic regression
# A tibble: 3 × 3
term estimate exp_estimate
<chr> <dbl> <dbl>
1 (Intercept) -0.315 0.729
2 arrival_date_day_of_month -0.00155 0.998
3 hotelResort Hotel -0.614 0.541Holding arrival day of month constant, the odds of Resort Hotel reservations being canceled is predicted to be lower by a factor of 0.541 compared to City Hotel reservations, on average.
Intercept in logistic regression
# A tibble: 3 × 3
term estimate exp_estimate
<chr> <dbl> <dbl>
1 (Intercept) -0.315 0.729
2 arrival_date_day_of_month -0.00155 0.998
3 hotelResort Hotel -0.614 0.541On the 0th day of the month, the odds of City Hotel reservations being canceled is predicted to be 0.729, on average. The intercept is not meaningful in this context since there is no 0th day of the month.
Cancellation ~ arrival date * hotel type
Fit another model to predict whether a reservation was cancelled from arrival_date_day_of_month and hotel type (Resort or City Hotel), allowing the relationship between arrival_date_day_of_month and is_canceled to vary based on hotel type.
is_canceled_fit_3 <- logistic_reg() |>
fit(is_canceled ~ arrival_date_day_of_month * hotel, data = hotels_train)
tidy(is_canceled_fit_3)# A tibble: 4 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -0.321 0.0172 -18.7 6.73e-78
2 arrival_date_day_of_month -0.00117 0.000954 -1.23 2.19e- 1
3 hotelResort Hotel -0.594 0.0313 -19.0 3.50e-80
4 arrival_date_day_of_month:hot… -0.00125 0.00174 -0.719 4.72e- 1Logistic regression w/ interaction effect
# A tibble: 4 × 2
term estimate
<chr> <dbl>
1 (Intercept) -0.321
2 arrival_date_day_of_month -0.00117
3 hotelResort Hotel -0.594
4 arrival_date_day_of_month:hotelResort Hotel -0.00125\[ \begin{aligned} \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) &= -0.321 \\ &- 0.00117 \times \texttt{arrival_date_day_of_month} \\ &- 0.594 \times \texttt{hotelResort Hotel} \\ &- 0.00125 \times \texttt{arrival_date_day_of_month:hotelResort Hotel} \\ \end{aligned} \]
Logistic regression w/ interaction effect
\[ \begin{aligned} \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) &= -0.321 \\ &- 0.00117 \times \texttt{arrival_date_day_of_month} \\ &- 0.594 \times \texttt{hotelResort Hotel} \\ &- 0.00125 \times \texttt{arrival_date_day_of_month:hotelResort Hotel} \\ \end{aligned} \]
City Hotel:
\[ \begin{aligned} \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) &= -0.321 \\ &- 0.00117 \times \texttt{arrival_date_day_of_month} \\ &- 0.594 \times 0 \\ &- 0.00125 \times \texttt{arrival_date_day_of_month} \times 0 \\ \\ &= -0.321 - 0.00117 \times \texttt{arrival_date_day_of_month} \\ \end{aligned} \]
Logistic regression w/ interaction effect
\[ \begin{aligned} \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) &= -0.321 \\ &- 0.00117 \times \texttt{arrival_date_day_of_month} \\ &- 0.594 \times \texttt{hotelResort Hotel} \\ &- 0.00125 \times \texttt{arrival_date_day_of_month:hotelResort Hotel} \\ \end{aligned} \]
Resort Hotel:
\[ \begin{aligned} \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) &= -0.321 \\ &- 0.00117 \times \texttt{arrival_date_day_of_month} \\ &- 0.594 \times 1 \\ &- 0.00125 \times \texttt{arrival_date_day_of_month} \times 1 \\ \\ &= -(0.321+0.594) - (0.00117+0.00125) \times \texttt{arrival_date_day_of_month} \\ \\ &= -0.915 - 0.00242 \times \texttt{arrival_date_day_of_month} \\ \end{aligned} \]
Logistic regression w/ interaction effect
City Hotel:
\[ \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) = -0.321 - 0.00117 \times \texttt{arrival_date_day_of_month} \]
exp(-0.00117)= 0.999: In City Hotels, for each day the booking is later in the month, the odds of reservations being canceled is predicted to be lower by a factor of 0.999, on average.exp(−0.321)= 0.725: In City Hotels, on the 0th day of the month, the odds of reservations being canceled is predicted to be 0.725, on average. The intercept is not meaningful in this context since there is no 0th day of the month.
Logistic regression w/ interaction effect
Resort Hotel:
\[ \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) = -0.915 - 0.00242 \times \texttt{arrival_date_day_of_month} \]
exp(-0.00117)= 0.998: In Resort Hotels, for each day the booking is later in the month, the odds of reservations being canceled is predicted to be lower by a factor of 0.998, on average.exp(−0.321)= 0.401: In Resort Hotels, on the 0th day of the month, the odds of reservations being canceled is predicted to be 0.401, on average. The intercept is not meaningful in this context since there is no 0th day of the month.
Participate 📱💻
Suppose we want to select a final model to predict whether a reservation was cancelled. Which metric would be most appropriate to evaluate the predictive performance of our logistic regression models?
- True positive rate
- Area under the ROC curve ✅
- Adjusted R-squared
- Root mean squared error
- R-squared

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Area under the ROC curve (AUC)
Single predictor:
Main effects:
Which model would you select as your final model based on AUC?
Linear regression
The dataset also contains information about the average daily rate (adr) for each reservation. The following model predicts adr from adults and hotel type.
# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 50.5 0.605 83.5 0
2 adults 29.5 0.311 94.9 0
3 hotelResort Hotel -10.7 0.322 -33.1 2.48e-239Participate 📱💻
Which of the following is the best interpretation of the slope coefficient for adults?
# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 50.5 0.605 83.5 0
2 adults 29.5 0.311 94.9 0
3 hotelResort Hotel -10.7 0.322 -33.1 2.48e-239For each additional adult in the booking, the average daily rate is predicted to be higher by $29.50
- on average, holding hotel type constant. ✅
- for Resort Hotels compared to City Hotels, on average.
- for City Hotels compared to Resort Hotels, on average.
- on average, not holding any other variables constant.

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Participate 📱💻
Which of the following is the correct interpretation of the slope coefficient for hotel?
# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 50.5 0.605 83.5 0
2 adults 29.5 0.311 94.9 0
3 hotelResort Hotel -10.7 0.322 -33.1 2.48e-239- For each additional Resort Hotel booking, the predicted average daily rate is $10.70 lower, holding number of adults constant.
- For each additional adult in the booking, the average daily rate is predicted to be lower by $10.70 for resort hotels compared to City Hotels, on average.
- Resort Hotels bookings are predicted to have an average daily rate that is $10.70 lower than City Hotels, on average, holding number of adults constant. ✅
- Resort Hotels bookings are predicted to have an average daily rate that is $10.70 higher than City Hotels, on average, holding number of adults constant.

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Participate 📱💻
Which of the following is the correct interpretation of the intercept?
# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 50.5 0.605 83.5 0
2 adults 29.5 0.311 94.9 0
3 hotelResort Hotel -10.7 0.322 -33.1 2.48e-239- The predicted average daily rate for a bookings with 0 adults at a Resort Hotel is $50.50, on average.
- The predicted average daily rate for a bookings with 0 adults at a City Hotel is $50.50, on average. ✅
- For each additional adult and Resort Hotel in the booking, the average daily rate is predicted to be $50.50 higher, on average.
- For each additional adult and City Hotel in the booking, the average daily rate is predicted to be $50.50 higher, on average.

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
Participate 📱💻
Which of the following (Plot A or Plot B) is the correct visual representation of this model?

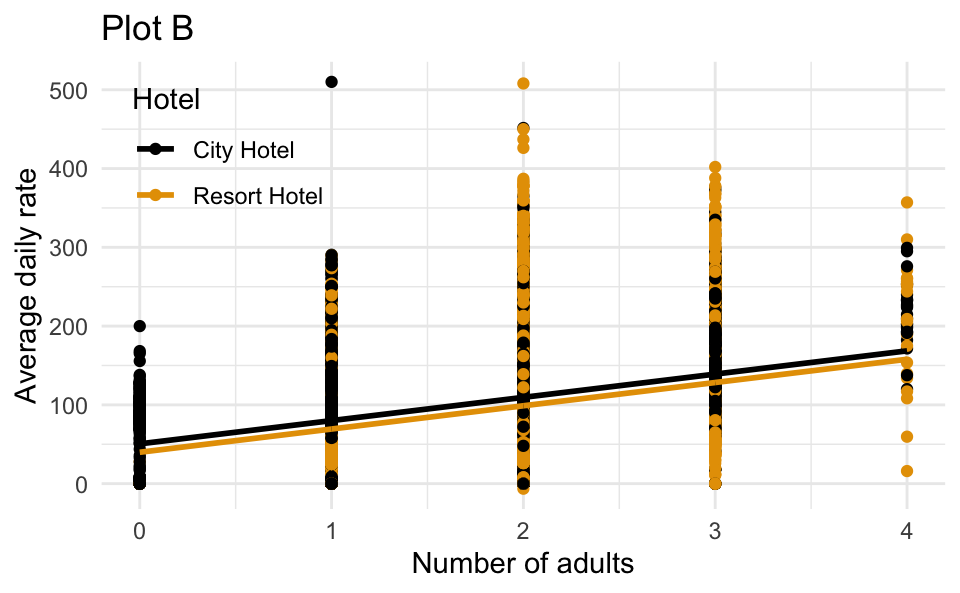
- Plot A
- Plot B ✅

Scan the QR code or go to app.wooclap.com/sta199. Log in with your Duke NetID.
